Groupes symétriques et groupes de permutations#

Nicolas M. Thiéry <Nicolas.Thiery at universite-paris-saclay.fr>

Groupe symétrique#

Definition 1 (Définition)

Soit \(E\) un ensemble.

On appelle groupe symétrique de \(E\) l’ensemble des applications bijectives de \(E\) sur \(E\) muni de la composition d’applications.

On le note \(S_E\) (variante classique \(\mathfrak S_E\)).

Exemple:

G = SymmetricGroup(['a', 'b', 'c'])
G.list()

Pour voir ses éléments comme des fonctions:

F = FiniteSetMaps(['a','b','c'])
F.domain()

F.codomain()

for sigma in G: print(F(sigma))

Cas particulier: groupe symmétrique d’ordre \(n\)#

Soit \(E\) l’ensemble fini \(\left\{ 1,\dots,n\right\}\), \(n\) étant un entier naturel strictement positif. On note alors \(S_n\) le groupe symétrique de cet ensemble. Les éléments de \(S_n\) sont appelés permutations et \(S_n\) est appelé groupe des permutations de degré \(n\), ou groupe symétrique d’indice \(n\).

Exemple:

S3 = SymmetricGroup(3)

Maintenant, si \(E\) est un ensemble à \(n\) éléments, alors on sait que \(S_E\) est isomorphe à \(S_n\):

G.is_isomorphic(S3)

En conséquence, il suffit de connaître les propriétés du groupe \(S_n\) pour en déduire celles du groupe \(S_E\).

Proposition

Le groupe \(S_n\) est d’ordre \(n!\) .

Exemple:

SymmetricGroup(3).cardinality()

SymmetricGroup(100).cardinality()

Permutations#

Quelques permutations particulières#

Definition 2

  • Une transposition \((i,j)\) est une permutation qui échange \(i\) et \(j\) et laisse les autres éléments inchangés.

  • Une transposition élémentaire est une transposition de la forme \((i,i+1)\).

  • Un cycle \((c_{1},c_{2},\dots,c_{k})\) est une permutation qui envoie \(c_{1}\) sur \(c_{2}\), \(c_{2}\) sur \(c_{3}\), et \(c_{k}\) sur \(c_{1}\).

Représentation des permutations#

G = SymmetricGroup(8)
sigma = G.random_element()

  • Mot:

[sigma(i) for i in range(1,9)]

sigma.domain()                            # raccourci mal nommé!

  • Bimot:

[(i,sigma(i)) for i in range(1,9)]

  • Graphe:

DiGraph([(i,sigma(i)) for i in range(1,9)], loops=True).plot()

DiGraph([(i,sigma(i)) for i in range(1,9)], loops=True).plot(talk=True)

  • Matrice:

sigma.matrix()

  • Produit de cycles (voir ci-dessous):

sigma

Produit de deux permutations#

Le produit dans le groupe symétrique est donné par la composition de fonctions: \(\sigma\tau = \sigma\circ\tau\). Parfois on préfère l’ordre inverse et on définit: \(\sigma \tau = \tau \circ \sigma\).

Exercice

Calculer le produit des permutations suivantes:

G = SymmetricGroup(3)
sigma = G([2,3,1])
tau   = G([2,1,3])

Solution

(sigma * tau).domain()

(tau * sigma).domain()

Note

Dans Sage, le produit sigma * tau désigne la composée \(\tau \circ \sigma\). Sage suit en cela la convention utilisée par le logiciel GAP, inclus dans Sage et à qui Sage délègue de nombreux calculs sur les groupes.

Propositions

  1. Dans le produit \(\sigma\tau\), on peut considérer que \(\tau\) permute les positions de \(\sigma\), tandis que dans le produit \(\tau\sigma\), \(\tau\) permute les valeurs de \(\sigma\):

G = SymmetricGroup(8)
tau   = G([(3,5)])
sigma = G([1,5,4,6,8,2,7,3])

(sigma * tau).domain()

(tau * sigma).domain()

Exercice

  1. Comment calculer l’inverse d’une permutation? Complexité?

  2. Calcul de la décomposition en cycles? Complexité?

Type cyclique#

Le type cyclique d’une permutation est la partition de \(n\) donnée par les longueurs de ses cycles.

sigma = G.random_element(); sigma

sigma.cycle_type()

Exercices

  1. Que se passe-t-il lorsque l’on conjugue une permutation \(\tau\) donnée sous forme de décomposition en cycles par une permutation \(\sigma\) (avec pour résultat \(\sigma\tau\sigma^{-1}\))?
    Indication: prendre \(\sigma = (1,2,3,4,5,6,7,8)\) et \(\tau=(2,5,3)\).

sigma = G([(1,2,3,4,5,6,7,8)])
tau   = G([(2,5,3)])
~sigma * tau * sigma

Solution

  1. Chaque cycle \((i_1,\dots,i_k)\) de \(\tau\) contribue un cycle \((\sigma(i_1),\dots,\sigma(i_k))\) dans \(\sigma\tau\sigma^{-1}\).

  2. Deux permutations sont dans la même classe de conjugaison si et seulement si elles ont même type cyclique. Les classes de conjugaisons sont donc indexées par les partitions.

Conséquence: les représentations du groupe symétrique sont indexées par les partitions.

Générateurs du groupe symétrique#

Proposition

  1. \(S_n\) est engendré par les cycles.

  2. \(S_n\) est engendré par les transpositions.

  3. \(S_n\) est engendré par les transpositions élémentaires \((i,i+1)\).

  4. \(S_n\) est engendré par la transposition \((1,2)\) et le cycle \((1,\dots,n)\).

Présentation par générateurs et relations#

Générateurs: \(\tau_{i}=(i,i+1)\).

Relations:

  • \(\tau_{i}^{2}=1\),

  • \(\tau_{i}\tau_{i+1}\tau_{i}=\tau_{i+1}\tau_{i}\tau_{i+1}\),

  • \(\tau_{i}\tau_{j}=\tau_{j}\tau_{i}\) si \(\left|i-j\right|>1\).

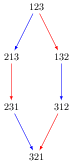
Le permutoèdre pour n=3

Fig. 1 Le permutoèdre pour \(S_3\)#

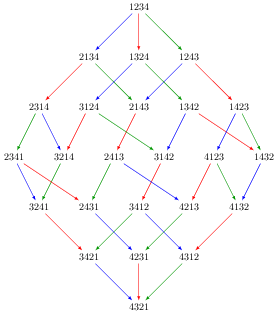
Le permutoèdre pour n=4

Fig. 2 Le permutoèdre pour \(S_4\)#

Exemple de lien combinatoire/algèbre: comptage des permutations par niveau et \(q\)-factorielle#

q = QQ['q'].gen()

1 * (1+q) * (1+q+q^2)

expand( 1 * (1+q) * (1+q+q^2) )

expand( 1 * (1+q) * (1+q+q^2) * (1+q+q^2+q^3) )

import sage.combinat.q_analogues
sage.combinat.q_analogues.q_factorial(4)

Les \(q\)-factorielles apparaissent aussi naturellement dans le comptage de sous-espaces vectoriels ou d’applications inversibles sur un corps fini \(\mathbb F_q\).

Groupes de permutations#

Definition 3

Un groupe de permutations est un groupe donné comme sous-groupe d’un groupe symétrique.

Exemples#

  • Groupe trivial \(id_n\).

  • Groupe cyclique \(C_n\):

C5 = CyclicPermutationGroup(5); C5

C5.group_generators()

  • Groupe diédral \(D_n\):

D5 = DihedralGroup(5); D5

D5.group_generators()

  • Groupe alterné \(A_n\):

A5 = AlternatingGroup(5); A5

A5.group_generators()

A5.is_simple()

  • Tout groupe fini! (théorème de Cayley)

Exercice

Construire le groupe des symétries du cube:

.                                    7-----8
.                                   /|    /|
.                                  5-----6 |
.                                  | |   | |
.                                  | 3---|-4
.                                  |/    |/
.                                  1-----2

G = PermutationGroup([...])

Applications#

  • Groupes de symétries d’objets discrets.

  • Comptage d’objets à isomorphie près (Énumération de Pólya; voir TP).

  • Étude des groupes finis.

  • Étude du groupe des permutations des racines d’un polynôme. C’est l’origine du concept de groupe par Évariste Galois.

Systèmes générateurs forts#

Problème: Soit \(G\subset S_n\) un groupe de permutation; \(G\) est typiquement très gros.

  1. Comment le représenter? Le manipuler?

  2. Calculer son nombre d’éléments?

  3. Tester si un élément est dedans?

  4. Exprimer un élément en fonction des générateurs?

  5. Déterminer ses sous-groupes?

  6. Est-il abélien, simple, résoluble, … ?

Exercice

Soit \(G\) un groupe de permutations de \(\{1,\dots,n\}\). Par exemple, le groupe des symétries du cube (\(n=8\)).

Soit \(H\) le sous groupe des éléments de \(G\) qui fixent \(n\).

  1. Supposons \(|H|\) connu. Comment en déduire \(|G|\)?

  2. Comment obtenir des représentants des classes de \(G/H\)?

  3. Supposons que l’on sache tester si une permutation est dans \(H\). Comment tester si une permutation est dans \(G\)?

Solution

Rappel: \(\quad\sigma H=\tau H \quad\Longleftrightarrow\quad \sigma^{-1}\tau\in H \quad\Longleftrightarrow\quad \sigma(n)=\tau(n)\)

Du coup, la fonction:

\[\begin{split} \phi: \begin{cases} G &\longmapsto G.n\\ g &\longrightarrow g(n) \end{cases} \end{split}\]

induit un isomorphisme entre les classes à droite \(\sigma H\) et les éléments de l’orbite \(G.n\) de \(n\) sous l’action de \(G\).

  1. \(|G| = |H|\ |G.x|\)

  2. Il suffit de choisir pour chaque \(j\) dans \(G.n\) une permutation \(\sigma_{n,j}\) telle que \(\sigma_{n,j}(n)=j\).

  3. Soit \(\sigma\) une permutation. Si \(\sigma(n)\not\in G.n\), alors \(\sigma\not\in G\). Sinon, \(\sigma_{n,\sigma(n)}^{-1} \sigma\) fixe \(n\). Donc \(\sigma \in G \Longleftrightarrow \sigma_{n,\sigma(n)}^{-1}\sigma\in H\).

On a une bonne idée? Appliquons la récursivement.

Définition

On considère la tour de groupes

\[ \{ id \} = G_0 \subset G_1 \subset \cdots \subset G_n = G\,, \]

où \(G_i:=G\cap S_i\) est le sous-groupe des éléments de \(G\) qui fixent \(\left\{i+1,\dots,n\right\}\).

Pour décrire \(G\), il suffit de décrire chacune des inclusions.

Un système générateur fort est composé des représentants \(\sigma_{i,j}\) des classes de \(G_{i}/G_{i-1}\) pour chaque \(i\).

On abrège système générateur fort en SGS (pour Strong Generating System).

Remarque

Un système générateur fort est un système générateur \(S\) adapté à la tour \(S_0 \subset S_1 \subset \cdots \subset S_n\):

\[\langle S\cap S_i\rangle = G \cap S_i = G_i\]

C’est l’analogue des bases sous forme échelon d’un espace vectoriel \(E\) qui sont adaptées à un drapeau.

Exemple

\(S_n\) engendré par toutes les transpositions.

Proposition

La connaissance d’un système générateur fort permet de résoudre tous les problèmes ci-dessus:

  1. Calcul du nombre d’éléments

  2. Test d’appartenance

  3. …

Exercices

  1. Construire à la main un système générateur fort pour:

    • le groupe trivial \(Id_n\)

    • le groupe cyclique \(C_4\)

    • le groupe alterné \(A_4\)

    • le groupe symétrique \(S_n\)

    • le groupe dihédral \(D_8\)

    • le groupe des symétries du cube agissant sur les sommets.

  2. Donner une borne sur la taille d’un système générateur fort. Comparer avec la taille du groupe.

PermutationGroup([], domain=[1,2,3,4]).strong_generating_system(base_of_group=[4,3,2,1])

CyclicPermutationGroup(4).strong_generating_system(base_of_group=[4,3,2,1])

AlternatingGroup(4).strong_generating_system(base_of_group=[4,3,2,1])

DihedralGroup(4).strong_generating_system(base_of_group=[4,3,2,1])

SymmetricGroup(4).strong_generating_system(base_of_group=[4,3,2,1])

Definition 4

Un sous-ensemble \(B\) est une base de \(G\) si tout élément \(g\) dans le groupe est caractérisé par \(g(b)\) pour \(b\) dans \(B\).

Ci-dessus, on a utilisé \(B:=\{n,\dots,1\}\), mais la définition de système générateur fort se généralise relativement à n’importe quelle base \(B\).

Exercices

  1. Vérifier que \(\left\{5,4,3\right\}\) est une base pour \(A_{5}\).

Algorithme de Schreier-Sims#

Comment calculer un système générateur fort?

  1. Calculer l’orbite \(G.n\) de \(n\) (comment on fait?).

  2. Les permutations \(\sigma_{n,j}\) qui envoient \(n\) sur \(j\), \(j\) dans \(G.n\) donnent des représentants des classes de \(G/G_n\).

  3. Calculer les générateurs de \(G_n\) avec le Lemme de Schreier (voir ci-dessous).

  4. Réitérer récursivement.

Lemme de Schreier

Soit \(G\) un groupe et \(H\) un sous-groupe. Soient \(A\) un ensemble de générateurs de \(G\) et \(U\) des représentants des \(H\)-classes à droite:

\[G = \langle A \rangle \qquad \text { et } G=\bigcup_{u\in U} uH,\]

Alors:

\[H = \langle v^{-1} a u \ \mid\ a\in A,\ u\in U \ \text{ et }\ v\in U,\ au\in vH \rangle\]

Démonstration

Soit \(g\in G\). On l’exprime en fonction des générateurs: \(g = a_1\cdots a_k\) avec les \(a_i\) dans \(A\).

Pour tout \(i\), prenons l’unique \(u_i\) tel que \(a_i\cdots a_k \in u_i H\). Alors:

\[g = a_1\cdots a_k = (a_1 u_2) (u_2^{-1}a_2u_3)(u_3^{-1}a_3u_4) \cdots (u_na_n)\,.\]

On note que chacun des facteurs est dans l’ensemble sus-mentionné. Ce dernier engendre donc \(H\).

Exercice:

Utiliser l’algorithme de Schreier-Sims pour retrouver un SGS pour le groupe des symétries du cube, sachant qu’il est engendré par \(\left(0,1,3,7,6,4\right)\left(2,5\right)\) et \(\left(0,1,3,2\right)\left(4,5,7,6\right)\).

Indication

Pour aller plus loin On peut calculer incrémentalement et efficacement un système générateur fort à partir d’un système générateur quelconque.

Algorithmes dérivés de petite complexité (typiquement \(O(n\log(|G|))\)). On peut manipuler des groupes de permutations d’ordre plusieurs centaines de milliers.

Exemple:

S3 = SymmetricGroup(3)

S3.subgroups()

Synthèse: méthodes d’éliminations#

Ce que l’on vient de voir est une idée très générale en calcul algébrique:

On a une structure algébrique:

  • une algèbre de polynômes (univariée/multivariée),

  • un espace vectoriel,

  • un groupe symétrique

  • …

On veut pouvoir calculer avec ses sous-structures \(I\) (idéaux, sous-espaces vectoriels, groupes de permutations):

  1. Test d’appartenance d’un élément à \(I\),

  2. Test d’égalité de \(I\) et de \(J\),

  3. Calcul de «taille» de \(I\),

  4. …

Pour cela, on se donne:

  1. Un ordre

  2. Un drapeau de sous-structures vis à vis de cet ordre

  3. Un procédé de division: Euclide, …

  4. Une notion de système générateur fort: PGCD, base de Gröbner, forme échelon, système fort de générateurs,

  5. Un algorithme de calcul d’un tel système: algorithme d’Euclide, de Buchberger, de Gauss, de Schreier-Sims, …

Quelques références#