La bibliothèque de Tsetlin#
Introduction#
Il est connu depuis quelques dizaines années que la théorie des représentations des groupes peut faciliter l’étude de systèmes dont l’évolution est aléatoire (chaînes de Markov), en les décomposant en systèmes plus simples. Plus récemment on a réalisé qu’en généralisant un peu le cadre (en remplaçant l’axiome d’inversibilité des groupes par d’autres axiomes) on pouvait expliquer le comportement particulièrement simple d’autres chaînes de Markov.
Dans ce texte, nous étudions une chaîne de Markov simple, la bibliothèque de Tsetlin, afin d’illustrer ce propos. C’est l’occasion de connecter entre eux quelques points clés du programme de l’agrégation: combinatoire, algèbre linéaire, représentations, chaînes de Markov, exploration informatique, sans demander de bagage théorique lourd.
La bibliothèque de Tsetlin#
Considérons un rayon d’une bibliothèque contenant \(n\) livres tous distincts. Lorsque l’on emprunte un livre pour le consulter, le règlement intérieur stipule que l’on doit le redéposer tout à la droite du rayon. C’est ce que l’on fait naturellement avec sa pile de chemises dans le placard: après usage et nettoyage d’une chemise, on la range en haut de la pile.
Ce mode d’organisation a l’intérêt d’être d’auto-adaptatif:
Les livres les plus souvent utilisés s’accumulent en bout de rayon, et sont donc très rapidement retrouvés.
Si l’usage évolue dans le temps, le système s’adapte.
De fait, ce type de stratégie est utilisé non seulement dans la vie courante, mais aussi dans des systèmes informatiques. Les questions naturelles qui se posent sont:
L”état stationnaire: Vers quel(s) état(s) converge le système? Cela afin, entre autres, d’évaluer le temps moyen d’accès à un livre.
La vitesse de convergence: à quelle vitesse le système s’adapte à un changement d’environnement.
Formalisons cela un peu. La bibliothèque de Tsetlin est la chaîne de Markov discrète (temps discret, espace d’état discret) décrite par:
Un ensemble \(\Omega_n\) d’états donné par les permutations des \(n\) livres.
Un ensemble d’opérations \(\tau_i: \Omega_n\mapsto \Omega_n\). Appliquer \(\tau_i\) à une permutation \(\sigma\) consiste à déplacer la valeur \(i\) à la fin de la permutation.
Des paramètres \(x_i\geq 0\), avec \(\sum_i x_i=1\), donnant à chaque itération la probabilité d’appliquer l’opération \(\tau_i\).
Graphe et matrice de transition#
On peut représenter l’ensemble \(\Omega_n\) muni des opérations \(\tau_i\) par un digraphe (essentiellement un automate); voici ce que l’on obtient pour \(n=3\) :
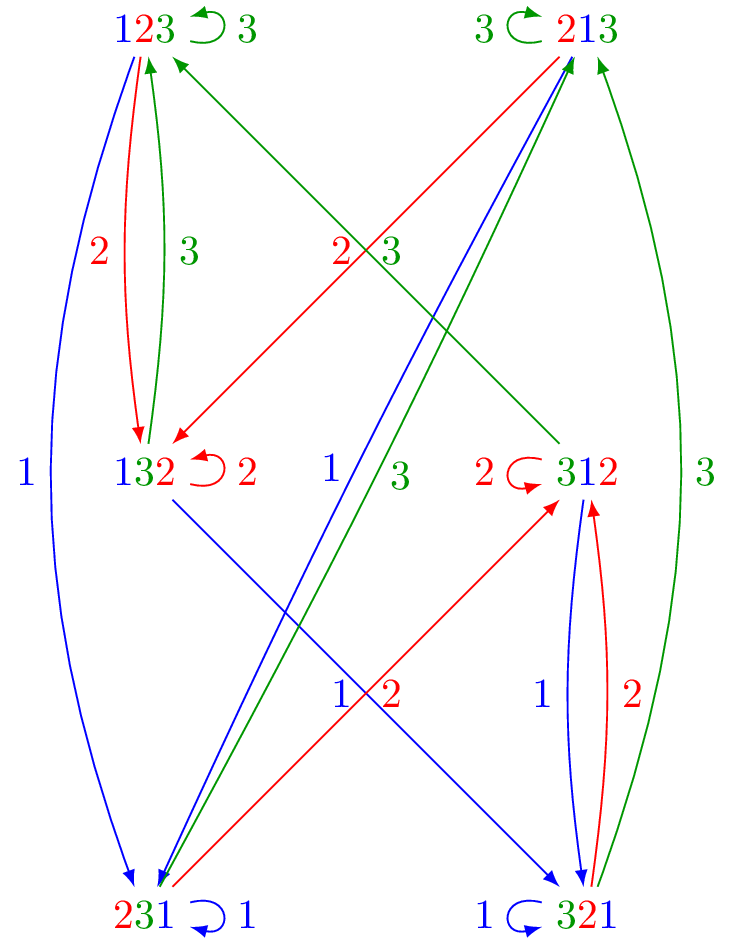
Exercice: étude du graphe/automate de transition#
Préciser que sigma(i): livre en position i
Pour des raisons techniques, il sera pratique de numéroter les livres par \(0,1,\cdots,n-1\), et de représenter chaque état de l’étagère par une permutation de \(\{0,\dots,n-1\}\) sous forme de tuple. Construire \(\Omega_n\) avec:
map(tuple, Permutations(range(3)))
Écrire une fonction tau(sigma, i) qui implante l’opération \(\tau_i\) en
prenant un tuple sigma et renvoyant un tuple sigma. Il peut être
pratique d’utiliser les opérations d’extractions de sous-tuples
(sigma[i:j]) et de concaténation.
mettre les bons paramètres à plot pour que ce soit moins moche
Écrire une fonction tsetlin_digraph(n) qui construit le (multi
digraphe) comme ci-dessus. Pour cela, on pourra construire la liste des
arêtes au moyen d’une compréhension, et la passer à DiGraph, en vous
inspirant de l’exemple suivant:
edges = [[i,i^2 % 10,"x"] for i in range(10)]
G = DiGraph(edges, loops=True)
G.plot(edge_labels=True)
Vérifier pour quelques valeurs de \(n\) que ce digraphe est fortement connexe. Cela indique que la chaîne de Markov est irréductible.
Linéarisation de la chaîne de Markov#
On souhaite non seulement manipuler des états, mais des combinaisons linéaires d’états, les coefficients représentant la probabilité d’être dans un état donné. Pour cela, on se fixe un corps \(K\) contenant les paramètres \(x_i\), et on considère l’espace vectoriel \(K\Omega_n\) dont la base est indexée par \(\Omega_n\).
On veut construire la matrice de transition qui décrit comment un élément de \(K\Omega_n\) est transformé à chaque itération. Autrement dit, c’est la matrice de l’opérateur \(\sum x_i \tau_i\), où chaque \(\tau_i\) est étendu par linéarité à tout \(K\Omega_n\).
Exercice: étude de la matrice de transition#
Implanter une fonction tsetlin_transition_matrix(n, x) qui étant donné
\(n\) et une liste de \(n\) paramètres construit la matrice de transition.
Mathématiquement, les lignes et colonnes de cette matrice sont indexées
par des permutations. Cependant Sage ne permet de construire que des
matrices aux lignes et colonnes indexées par des entiers. Pour passer
d’une indexation à l’autre, on pourra avantageusement utiliser la
fonction sage.combinat.ranker.rank_from_list :
r = sage.combinat.ranker.rank_from_list(['a',1,x])
r('a')
r(1)
r(x)
Indication: selon les paramètres, on voudra construire une matrice à coefficients entiers, rationnels, symboliques. On pourra supposer que tous les paramètres vivent dans le même anneau, donné par \(x[0].parent()\), et construire la matrice en conséquence.
Tester votre fonction pour \(n=3\) en prenant comme liste de paramètres:
x = var(['x%i'%i for i in range(3)])
Vérifier que, en prenant \(x_i=1\) pour tout \(i\), on retrouve la matrice d’adjacence du graphe de transition.
Vérifier que la matrice est stochastique.
Vérifier que \(\sum_i x_i\) (c’est-à-dire \(1\) en principe) est valeur propre de multiplicité \(1\) et calculer le vecteur propre associé. Que représente ce vecteur propre? Pourquoi la multiplicité doit être \(1\)?
Jusqu’où peut-on aller? Quelle est la difficulté?
Pour tester plus loin, prendre par exemple \(x_i = 1/n\). Jusqu’où peut-on aller? Quelle est la difficulté?
Combien y-a-t’il de coefficients non nuls dans la matrice de transition? Et après application du pivot de Gauß?
Comment pousser plus loin?
Calculer les valeurs propres de la matrice de transition (méthode
eigenvalues).
Que remarquez-vous?
Quelles stratégies peut-on appliquer pour pousser le calcul aussi loin que possible?
R-trivialité et conséquences#
On rappelle qu’un monoïde est un ensemble muni d’une loi associative admettant un élément neutre. L’ensemble \(T_n\) des fonctions de \(\Omega_n\) dans \(\Omega_n\) est un monoïde pour la composition. On appelle monoïde de transition le sous-monoïde \(M_n\) engendré par les \(\tau_i\).
Exercice: le monoïde de transition est \(R\)-trivial#
Construire le monoïde \(T_n\) des fonctions de \(\Omega_n\) dans \(\Omega_n\)
en utilisant FiniteSetMaps. Choisir une action à gauche pour avoir la
loi de composition dans l’ordre usuel. Construire aussi la fonction
identité avec la méthode one.
Construire chaque \(\tau_i\) comme un élément de \(T_n\). Les stocker dans
une liste tau. Indication: que font les commandes suivantes:
import functools
f = functools.partial(tau, i=2)
f( (2, 1, 3) )
En utilisant TransitiveIdeal, construire la liste des éléments du
monoïde \(M_n\) comme le plus petit ensemble contenant l’identité de \(T_n\)
et stable par multiplication à gauche par les \(\tau_i\). Indication:
définir une fonction suivants(m) qui étant donné un élément \(m\) de
\(T_n\) renvoie la liste de tous les produits \(m \tau_i\).
Construire le graphe de Cayley à droite de \(M_n\) (voir
Graphe_de_Cayley). C’est-à-dire le digraphe ayant comme sommets les
éléments de \(M_n\) et comme arêtes les \(m
\stackrel{i}{\rightarrow} m\tau_i\).
Vérifier, pour de petites valeurs de \(n\), que le graphe de Cayley de \(M_n\) est acyclique. C’est la propriété de \(R\)-trivialité.
Application#
En terme de théorie des représentations le fait que le monoïde \(M_n\) soit \(R\)-trivial implique que ses modules simples sont de dimension \(1\). Considérons alors le \(M_n\)-module \(K\Omega\). Il existe une suite de composition maximale pour \(K\Omega\); c’est-à-dire une suite de \(M_n\)-modules emboîtés:
telle que \(V_i/V_{i-1}\) est un module simple. Ceux ci étant de dimension \(1\), les \(V_i\) forment un drapeau complet dans \(K\Omega_n\) stabilisé par \(M_n\).
Plus prosaïquement, cela se traduit par l’existence d’une base adaptée de \(K\Omega_n\) dans laquelle tous les éléments de \(M_n\) sont triangulaires supérieurs (c’est un analogue de la diagonalisation simultanée d’un ensemble de matrices commutant entre elles). Cette base n’est pas forcément aisée à construire, mais nous avons uniquement besoin de son existence!
Exercice: caractérisation des valeurs propres possibles de \(M\)#
Déduire de la \(R\)-trivialité de \(M\) que les valeurs propres de la matrice de transition sont toutes de la forme \(\sum_{i\in S} x_i\), où \(S\) est un sous-ensemble de \(\{1,\dots,n\}\). Indication: vérifier que chaque opérateur \(\tau_i\) est idempotent, et en déduire ses valeurs propres.
Exercice: une conjecture pour les valeurs propres et leur multiplicité#
Prendre comme paramètres \(x_i = 2^i\) et choisir un nombre premier \(p\) strictement supérieur à \(2^n\).
Construire la matrice de transition, avec ces paramètres, et dans le corps \(\ZZ/p\ZZ\). Calculer ses valeurs propres avec leur multiplicités.
Montrer que ce calcul est suffisant pour déterminer les valeurs propres de la matrice de transition pour des paramètres formels.
Calculer les multiplicités obtenues pour quelques valeurs de \(n\), les regarder en détail, et formuler une conjecture. Indication: utiliser l”Encyclopédie en Ligne des Séquences d’Entiers.
Exercice: Détermination des valeurs propres et leur multiplicité par la théorie des caractères#
Nous allons retrouver combinatoirement les valeurs propres et leur multiplicités. Le principe est que, la matrice étant triangulaire, il suffit de connaître ses coefficients diagonaux, c’est-à-dire comment elle agit sur les quotients \(V_i/V_{i-1}\). Autrement dit, on a uniquement besoin de connaître la multiplicité des modules simples dans \(K\Omega\), et ceci peut se faire, comme pour les groupes, par théorie des caractère: on va compter des points fixes puis inverser par la table des caractères.
Il se trouve que, pour un monoïde \(R\)-trivial, la table des caractères est uni-triangulaire supérieure à coefficients 0-1: c’est la matrice d’incidence d’un ordre partiel \(P\). L’inverser revient donc à une inversion de Möbius par rapport à \(P\). Pour le monoïde \(M_n\) l’ordre partiel est simplement le treillis booléen des sous-ensembles de \(\{0,\dots,n\}\) et l’inversion de Möbius est donc juste une inclusion exclusion.
Pour \(S\) un sous-ensemble de \(\{0,\dots,n\}\), on définit l’opérateur \(\tau_S:=\prod_i \tau_i\), où le produit est pris dans l’ordre croissant (par exemple). Ainsi, \(\tau_{\{1,3\}}=\tau_1\circ\tau_3\).
Les éléments \(\tau_S\) jouent le rôle des représentants des classes de conjugaison.
Chacun des points suivant est à effectuer au choix théoriquement par ordinateur sur des exemples, ou pour \(n\) quelconque.
Vérifier que \(\tau_S\) est idempotent.
Compter le nombre \(c_S\) de points fixes de chaque \(\tau_S\).
Appliquer l’inclusion-exclusion \(m_S = \sum_{S'\supseteq S} c_S\) et constater que \(m_S\) redonne la multiplicité des valeurs propres \(\sum_{i\in S} x_i\) de la conjecture.
Conclusion#
Les prémisses de cette approche des chaînes de Markov remontent à l’étude de la bibliothèque de Tsetlin par [Bidigare_1997], [Brown_2000] … Cela a fortement contribué à l’engouement récent pour l’étude de la théorie des représentations des monoïdes. On pourra par exemple se référer à [ASST_2014] pour une liste de références, ainsi qu’une étude un peu systématique de cette approche dans le cas R-trivial et son application à l’étude de plusieurs familles de chaînes de Markov; cela inclus des modèles dans la mouvance des «tas de sable» qui modélisent en physique statistique des phénomènes comme les avalanches [ASST_2013].
ASST_2013
Directed nonabelian sandpile models on trees Ayyer, Arvind and
Schilling, Anne and Steinberg, Benjamin and Thiéry, Nicolas M.
arXiv:1305.1697
ASST_2014
Markov chains, \(R\)-trivial monoids and representation theory Ayyer,
Arvind and Schilling, Anne and Steinberg, Benjamin and Thiéry, Nicolas
M. arXiv:1401.4250
Bidigare_1997
Thomas Patrick Bidigare. Hyperplane arrangement face algebras and their
associated Markov chains. ProQuest LLC, Ann Arbor, MI, 1997. Thesis
(Ph.D.)–University of Michigan.
Brown_2000
Kenneth S. Brown. Semigroups, rings, and Markov chains. J. Theoret.
Probab., 13(3):871–938, 2000.
